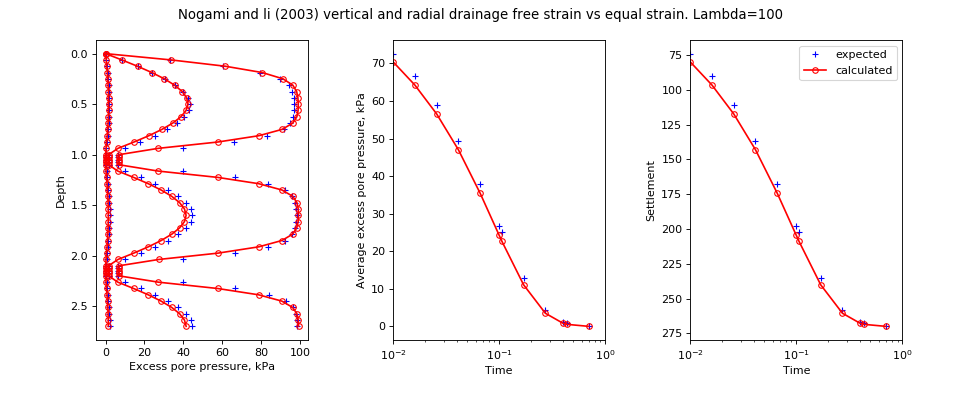
speccon example code: speccon1d_vr_vert_and_radial_equal_vs_free_strain_nogmaiandli2003.py¶
# speccon1d_vr example (if viewing this in docs, plots are at bottom of page)
# Vertical and radial consolidation of clay with thin sand layers.
# Compare free strain solution of Nogami and Li (2003) with the equal strain
# solutin of speccon1d_vr. This is similar to Figure 10c) from the article.
# The orignal solution of Nogami and Li (2003)
# is implemented separately in geotecha.consolidation.nogamiandli2003
# Nogami, Toyoaki, and Maoxin Li. (2003) 'Consolidation of Clay with a
# System of Vertical and Horizontal Drains'. Journal of
# Geotechnical and Geoenvironmental Engineering 129, no. 9
# 838-48. doi:10.1061/(ASCE)1090-0241(2003)129:9(838).
# This file should be run with python. It will not work if run with the
# speccon1d_vr.exe script program.
from __future__ import division, print_function
import numpy as np
from geotecha.speccon.speccon1d_vr import Speccon1dVR
import matplotlib.pyplot as plt
#Expected values
#t = time values
#avp = average excess pore pressure
#z = depth values
#por = excess pore pressure at time t and depth z.
#settle = settlement
t = np.array([ 0.01 , 0.01603286, 0.02570525, 0.04121285, 0.06607597,
0.1, 0.10593866, 0.16984993, 0.27231794, 0.4, 0.43660343, 0.7 ])
z = np.array(
[ 0. , 0.0625, 0.125 , 0.1875, 0.25 , 0.3125, 0.375 ,
0.4375, 0.5 , 0.5625, 0.625 , 0.6875, 0.75 , 0.8125,
0.875 , 0.9375, 1. , 1.025 , 1.05 , 1.075 , 1.1 ,
1.1625, 1.225 , 1.2875, 1.35 , 1.4125, 1.475 , 1.5375,
1.6 , 1.6625, 1.725 , 1.7875, 1.85 , 1.9125, 1.975 ,
2.0375, 2.1 , 2.125 , 2.15 , 2.175 , 2.2 , 2.2625,
2.325 , 2.3875, 2.45 , 2.5125, 2.575 , 2.6375, 2.6999 ])
por = np.array(
[[ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[ 3.30085802e+01, 8.39070407e+00, 3.58707855e-01],
[ 6.05040116e+01, 1.64657476e+01, 7.03954600e-01],
[ 7.93733840e+01, 2.39216010e+01, 1.02278441e+00],
[ 8.98276000e+01, 3.04784367e+01, 1.30323304e+00],
[ 9.44368466e+01, 3.58906380e+01, 1.53477694e+00],
[ 9.61739263e+01, 3.99558431e+01, 1.70872820e+00],
[ 9.69096134e+01, 4.25222425e+01, 1.81856068e+00],
[ 9.72060228e+01, 4.34939559e+01, 1.86015483e+00],
[ 9.70563632e+01, 4.28344044e+01, 1.83195234e+00],
[ 9.64675854e+01, 4.05676349e+01, 1.73501446e+00],
[ 9.51338553e+01, 3.67775792e+01, 1.57298210e+00],
[ 9.15678072e+01, 3.16052348e+01, 1.35193903e+00],
[ 8.28664682e+01, 2.52437753e+01, 1.08018340e+00],
[ 6.59357468e+01, 1.79316479e+01, 7.67916132e-01],
[ 3.96855349e+01, 9.94380297e+00, 4.26857907e-01],
[ 6.59655749e+00, 1.58132211e+00, 6.98091328e-02],
[ 6.59134099e+00, 1.58005846e+00, 6.97557684e-02],
[ 6.58961224e+00, 1.57964519e+00, 6.97399004e-02],
[ 6.59137041e+00, 1.58008208e+00, 6.97615203e-02],
[ 6.59661708e+00, 1.58136940e+00, 6.98206398e-02],
[ 3.98547617e+01, 1.00628681e+01, 4.55528866e-01],
[ 6.63377268e+01, 1.81728261e+01, 8.24478652e-01],
[ 8.35306351e+01, 2.56128437e+01, 1.16311926e+00],
[ 9.24242085e+01, 3.21098488e+01, 1.45901394e+00],
[ 9.60705684e+01, 3.74261238e+01, 1.70129661e+00],
[ 9.74392519e+01, 4.13677993e+01, 1.88107072e+00],
[ 9.81005003e+01, 4.37915763e+01, 1.99173594e+00],
[ 9.83479591e+01, 4.46095565e+01, 2.02923036e+00],
[ 9.81079539e+01, 4.37921401e+01, 1.99217957e+00],
[ 9.74436874e+01, 4.13689901e+01, 1.88194701e+00],
[ 9.60657415e+01, 3.74280676e+01, 1.70258384e+00],
[ 9.24170918e+01, 3.21127333e+01, 1.46068005e+00],
[ 8.35319659e+01, 2.56169153e+01, 1.16512240e+00],
[ 6.63469036e+01, 1.81783823e+01, 8.26768047e-01],
[ 3.98602199e+01, 1.00702443e+01, 4.58045763e-01],
[ 6.59182174e+00, 1.59091774e+00, 7.24995316e-02],
[ 6.58658179e+00, 1.58963382e+00, 7.24411588e-02],
[ 6.58484730e+00, 1.58920618e+00, 7.24217283e-02],
[ 6.58661723e+00, 1.58963460e+00, 7.24412296e-02],
[ 6.59189335e+00, 1.59091932e+00, 7.24996732e-02],
[ 4.00379871e+01, 1.00742370e+01, 4.58399695e-01],
[ 6.66669810e+01, 1.81862162e+01, 8.27472042e-01],
[ 8.39318565e+01, 2.56282977e+01, 1.16616892e+00],
[ 9.28276558e+01, 3.21272424e+01, 1.46205756e+00],
[ 9.64383871e+01, 3.74451724e+01, 1.70427658e+00],
[ 9.77664761e+01, 4.13880757e+01, 1.88393471e+00],
[ 9.83983815e+01, 4.38125372e+01, 1.99443713e+00],
[ 9.86319025e+01, 4.46305720e+01, 2.03172745e+00]])
avp = np.array(
[[ 7.25979052e+01, 6.65166314e+01, 5.89096834e+01,
4.94554633e+01, 3.79564622e+01, 2.66323138e+01,
2.50358034e+01, 1.28862133e+01, 4.44927613e+00,
1.18311566e+00, 8.09339892e-01, 5.26895921e-02]])
settle = np.array(
[[ 73.98565603, 90.40509513, 110.94385476, 136.47024905,
167.51755212, 198.09275262, 202.40333078, 235.20722417,
257.98695445, 266.80558772, 267.81478229, 269.8577381 ]])
#################################################
##nogami and li parameters to generate expected values
#surcharge_vs_time = PolyLine([0,0,10], [0,100,100])
#hs=0.05
#h = np.array([1, hs, hs, 1, hs, hs, 0.5])
#lam = 100
#kv = np.array([1,lam/hs, lam/hs, 1, lam/hs, lam/hs, 1])
#mv = np.array([1.0, 1, 1, 1, 1, 1, 1])
#kh = kv
#
#r0 = 0.05
#r1 = 20 * r0
##z = layer_coords(h, 45,2)
#
#bctop = 0
#bcbot = 1
#nv = 15
#nh = 5
#
#tpor = np.array([0.01,0.1, 0.4])
#
#z = np.array(
# [ 0. , 0.0625, 0.125 , 0.1875, 0.25 , 0.3125, 0.375 ,
# 0.4375, 0.5 , 0.5625, 0.625 , 0.6875, 0.75 , 0.8125,
# 0.875 , 0.9375, 1. , 1.025 , 1.05 , 1.075 , 1.1 ,
# 1.1625, 1.225 , 1.2875, 1.35 , 1.4125, 1.475 , 1.5375,
# 1.6 , 1.6625, 1.725 , 1.7875, 1.85 , 1.9125, 1.975 ,
# 2.0375, 2.1 , 2.125 , 2.15 , 2.175 , 2.2 , 2.2625,
# 2.325 , 2.3875, 2.45 , 2.5125, 2.575 , 2.6375, 2.6999 ])
#
#
#t = np.array(
# [ 0.01 , 0.01603286, 0.02570525, 0.04121285, 0.06607597,
# 0.1, 0.10593866, 0.16984993, 0.27231794, 0.4, 0.43660343, 0.7 ])
#
#max_iter=20000
#vertical_roots_x0 = 2.2
#vertical_roots_dx = 1e-3
#vertical_roots_p = 1.01
#################################################
reader = ("""\
surcharge_vs_time = PolyLine([0,0,10], [0,100,100])
hs=0.05
h = np.array([1, hs, hs, 1, hs, hs, 0.5])
lam = 100
kv = np.array([1,lam/hs, lam/hs, 1, lam/hs, lam/hs, 1])
mv = np.array([1.0, 1, 1, 1, 1, 1, 1])
kh = kv
tpor = np.array([0.01,0.1, 0.4])
z = np.array(
[ 0. , 0.0625, 0.125 , 0.1875, 0.25 , 0.3125, 0.375 ,
0.4375, 0.5 , 0.5625, 0.625 , 0.6875, 0.75 , 0.8125,
0.875 , 0.9375, 1. , 1.025 , 1.05 , 1.075 , 1.1 ,
1.1625, 1.225 , 1.2875, 1.35 , 1.4125, 1.475 , 1.5375,
1.6 , 1.6625, 1.725 , 1.7875, 1.85 , 1.9125, 1.975 ,
2.0375, 2.1 , 2.125 , 2.15 , 2.175 , 2.2 , 2.2625,
2.325 , 2.3875, 2.45 , 2.5125, 2.575 , 2.6375, 2.6999 ])
t = np.array(
[ 0.01 , 0.01603286, 0.02570525, 0.04121285, 0.06607597,
0.1, 0.10593866, 0.16984993, 0.27231794, 0.4, 0.43660343, 0.7 ])
z2 = np.cumsum(h)
z1 = z2-h
H = np.sum(h)
z1/=H
z2/=H
kv = PolyLine(z1, z2, kv, kv)
mv = PolyLine(z1, z2, mv, mv)
kh = kv
drn = 1
neig=80
mvref=1.0
surcharge_vs_depth = mv
#rw=0.05, re = 20*rw = 1.0, n=20, no smear zone
#Therfore muI=2.253865374, eta = 2/mu/re**2 = 0.887364446
etref = 0.887364446
et = PolyLine(z1, z2, np.ones_like(z1), np.ones_like(z1))
dTv = 1/H**2
dTh = etref
ppress_z = np.array(
[ 0. , 0.0625, 0.125 , 0.1875, 0.25 , 0.3125, 0.375 ,
0.4375, 0.5 , 0.5625, 0.625 , 0.6875, 0.75 , 0.8125,
0.875 , 0.9375, 1. , 1.025 , 1.05 , 1.075 , 1.1 ,
1.1625, 1.225 , 1.2875, 1.35 , 1.4125, 1.475 , 1.5375,
1.6 , 1.6625, 1.725 , 1.7875, 1.85 , 1.9125, 1.975 ,
2.0375, 2.1 , 2.125 , 2.15 , 2.175 , 2.2 , 2.2625,
2.325 , 2.3875, 2.45 , 2.5125, 2.575 , 2.6375, 2.6999 ])
ppress_z/=H
avg_ppress_z_pairs = [[0,1]]
settlement_z_pairs = [[0,1]]
tvals = np.array(
[ 0.01 , 0.01603286, 0.02570525, 0.04121285, 0.06607597,
0.1, 0.10593866, 0.16984993, 0.27231794, 0.4, 0.43660343, 0.7 ])
ppress_z_tval_indexes = [0, 5, 9] #0.01, 0.1, 0.4
""")
a = Speccon1dVR(reader)
a.make_all()
# custom plots
title = ("Nogami and li (2003) vertical and radial drainage"
" free strain vs equal strain. Lambda=100")
fig = plt.figure(figsize=(12,5))
fig.suptitle(title)
#z vs u
ax1 = fig.add_subplot("131")
ax1.set_xlabel('Excess pore pressure, kPa')
ax1.set_ylabel('Depth')
ax1.invert_yaxis()
ax1.plot(por, z,
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax1.plot(a.por, z,
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
# avp vs t
ax2 = fig.add_subplot("132")
ax2.set_xlabel('Time')
ax2.set_ylabel('Average excess pore pressure, kPa')
ax2.set_xscale('log')
ax2.set_xlim((0.01, 1))
ax2.plot(t, avp[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax2.plot(t, a.avp[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
# settlement vs t
ax3 = fig.add_subplot("133")
ax3.set_xlabel('Time')
ax3.set_ylabel('Settlement')
ax3.invert_yaxis()
ax3.set_xscale('log')
ax3.set_xlim((0.01, 1))
ax3.plot(t, settle[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax3.plot(t, a.set[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
leg = ax3.legend()
leg.draggable()
fig.subplots_adjust(top=0.90, bottom=0.15, left=0.1, right=0.94, wspace=0.4)
#fig.tight_layout()
plt.show()
(Source code, png, hires.png, pdf)