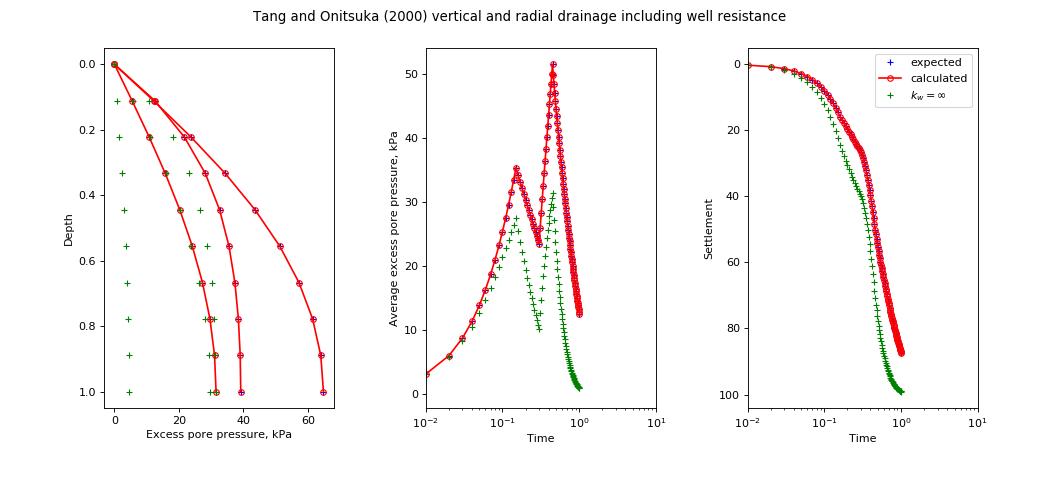
speccon example code: speccon1d_vrw_vert_and_radial_with_well_resis_drainage_tangandonitsuka2000.py¶
# speccon1d_vrw example (if viewing this in docs, plots are at bottom of page)
# Reproduce solution of Tang and Onitsuka (2000) which includes vertical and
# radial drainage as well as well resistance in a unit cell.
#The orignal solution of Tang and Onitsuka
# (2000) is implemented separately in
# geotecha.consolidation.tangandonituka2000.
# Tang, Xiao-Wu, and Katsutada Onitsuka. (2000) 'Consolidation by
# vertical drains under Time-Dependent Loading'. Int
# Journal for Numerical and Analytical Methods in
# Geomechanics 24, no. 9 (2000): 739-51.
# doi:10.1002/1096-9853(20000810)24:9<739::AID-NAG94>3.0.CO;2-B.
# This file should be run with python. It will not work if run with the
# speccon1d_vr.exe script program.
from __future__ import division, print_function
import numpy as np
from geotecha.speccon.speccon1d_vrw import Speccon1dVRW
import matplotlib.pyplot as plt
#Expected values
#t = time values
#avp = average excess pore pressure
#z = depth values
#por = excess pore pressure at time t and depth z.
#settle = settlement
t = np.array([ 1.00000000e-03, 2.00000000e-03, 3.00000000e-03,
4.00000000e-03, 5.00000000e-03, 6.00000000e-03,
7.00000000e-03, 8.00000000e-03, 9.00000000e-03,
1.00000000e-02, 2.00000000e-02, 3.00000000e-02,
4.00000000e-02, 5.00000000e-02, 6.00000000e-02,
7.00000000e-02, 8.00000000e-02, 9.00000000e-02,
1.00000000e-01, 1.10000000e-01, 1.20000000e-01,
1.30000000e-01, 1.40000000e-01, 1.50000000e-01,
1.60000000e-01, 1.70000000e-01, 1.80000000e-01,
1.90000000e-01, 2.00000000e-01, 2.10000000e-01,
2.20000000e-01, 2.30000000e-01, 2.40000000e-01,
2.50000000e-01, 2.60000000e-01, 2.70000000e-01,
2.80000000e-01, 2.90000000e-01, 3.00000000e-01,
3.10000000e-01, 3.20000000e-01, 3.30000000e-01,
3.40000000e-01, 3.50000000e-01, 3.60000000e-01,
3.70000000e-01, 3.80000000e-01, 3.90000000e-01,
4.00000000e-01, 4.10000000e-01, 4.20000000e-01,
4.30000000e-01, 4.40000000e-01, 4.50000000e-01,
4.60000000e-01, 4.70000000e-01, 4.80000000e-01,
4.90000000e-01, 5.00000000e-01, 5.10000000e-01,
5.20000000e-01, 5.30000000e-01, 5.40000000e-01,
5.50000000e-01, 5.60000000e-01, 5.70000000e-01,
5.80000000e-01, 5.90000000e-01, 6.00000000e-01,
6.10000000e-01, 6.20000000e-01, 6.30000000e-01,
6.40000000e-01, 6.50000000e-01, 6.60000000e-01,
6.70000000e-01, 6.80000000e-01, 6.90000000e-01,
7.00000000e-01, 7.10000000e-01, 7.20000000e-01,
7.30000000e-01, 7.40000000e-01, 7.50000000e-01,
7.60000000e-01, 7.70000000e-01, 7.80000000e-01,
7.90000000e-01, 8.00000000e-01, 8.10000000e-01,
8.20000000e-01, 8.30000000e-01, 8.40000000e-01,
8.50000000e-01, 8.60000000e-01, 8.70000000e-01,
8.80000000e-01, 8.90000000e-01, 9.00000000e-01,
9.10000000e-01, 9.20000000e-01, 9.30000000e-01,
9.40000000e-01, 9.50000000e-01, 9.60000000e-01,
9.70000000e-01, 9.80000000e-01, 9.90000000e-01,
1.00000000e+00, 1.01000000e+00])
avp = np.array([[ 0.32511915, 0.64395023, 0.95850548, 1.26960191,
1.57771242, 1.88315609, 2.1861672 , 2.48692722,
2.78558219, 3.0822529 , 5.95702388, 8.69654086,
11.32667999, 13.86239625, 16.31378009, 18.68823918,
20.9915131 , 23.22821996, 25.40218126, 27.51662947,
29.5743482 , 31.57777121, 33.52905472, 35.43013181,
34.20050107, 33.13149968, 32.15237839, 31.23863626,
30.37660619, 29.55741125, 28.77479332, 28.02410687,
27.30177917, 26.60499098, 25.93147359, 25.27937235,
24.6471508 , 24.03352086, 23.43739069, 25.94007773,
28.25103728, 30.44178874, 32.53758204, 34.5528131 ,
36.4970684 , 38.37729705, 40.19881778, 41.9658593 ,
43.6818802 , 45.34977247, 46.97199843, 48.55068709,
50.08770434, 51.58470557, 49.96092296, 48.5074373 ,
47.15325214, 45.8736276 , 44.65466537, 43.48726435,
42.36494895, 41.28286238, 40.23722658, 39.2250226 ,
38.24378734, 37.29147691, 36.36637054, 35.46700056,
34.59210015, 33.74056327, 32.91141376, 32.10378096,
31.31688056, 30.54999935, 29.80248297, 29.07372621,
28.36316519, 27.67027097, 26.99454454, 26.33551264,
25.69272447, 25.06574893, 24.45417241, 23.857597 ,
23.27563895, 22.70792745, 22.15410362, 21.61381963,
21.08673795, 20.57253078, 20.07087947, 19.5814741 ,
19.10401306, 18.6382027 , 18.18375701, 17.74039736,
17.3078522 , 16.88585686, 16.47415334, 16.07249005,
15.68062171, 15.29830908, 14.92531886, 14.5614235 ,
14.20640105, 13.86003501, 13.5221142 , 13.1924326 ,
12.87078925, 12.55698809]])
z = np.array(
[ 0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ])
por = np.array(
[[ 0. , 0. , 0. ],
[ 12.53440575, 12.14329557, 5.47538418],
[ 21.70121334, 23.7536632 , 10.78420485],
[ 28.183674 , 34.3627168 , 15.76501214],
[ 32.61240467, 43.61300164, 20.26641403],
[ 35.52623848, 51.27538849, 24.15169042],
[ 37.36067128, 57.23734454, 27.30293317],
[ 38.44529475, 61.47089757, 29.62459012],
[ 39.00780593, 63.99300069, 31.04631563],
[ 39.18082801, 64.82986237, 31.52505531]])
settle = (np.interp(t,[0,0.15,0.3,0.45,4], [0.0,50,50,100,100]) - avp)
#########################################
#Tang and onitsuka input to generate expected values
#t = np.array([ 1.00000000e-03, 2.00000000e-03, 3.00000000e-03,
# 4.00000000e-03, 5.00000000e-03, 6.00000000e-03,
# 7.00000000e-03, 8.00000000e-03, 9.00000000e-03,
# 1.00000000e-02, 2.00000000e-02, 3.00000000e-02,
# 4.00000000e-02, 5.00000000e-02, 6.00000000e-02,
# 7.00000000e-02, 8.00000000e-02, 9.00000000e-02,
# 1.00000000e-01, 1.10000000e-01, 1.20000000e-01,
# 1.30000000e-01, 1.40000000e-01, 1.50000000e-01,
# 1.60000000e-01, 1.70000000e-01, 1.80000000e-01,
# 1.90000000e-01, 2.00000000e-01, 2.10000000e-01,
# 2.20000000e-01, 2.30000000e-01, 2.40000000e-01,
# 2.50000000e-01, 2.60000000e-01, 2.70000000e-01,
# 2.80000000e-01, 2.90000000e-01, 3.00000000e-01,
# 3.10000000e-01, 3.20000000e-01, 3.30000000e-01,
# 3.40000000e-01, 3.50000000e-01, 3.60000000e-01,
# 3.70000000e-01, 3.80000000e-01, 3.90000000e-01,
# 4.00000000e-01, 4.10000000e-01, 4.20000000e-01,
# 4.30000000e-01, 4.40000000e-01, 4.50000000e-01,
# 4.60000000e-01, 4.70000000e-01, 4.80000000e-01,
# 4.90000000e-01, 5.00000000e-01, 5.10000000e-01,
# 5.20000000e-01, 5.30000000e-01, 5.40000000e-01,
# 5.50000000e-01, 5.60000000e-01, 5.70000000e-01,
# 5.80000000e-01, 5.90000000e-01, 6.00000000e-01,
# 6.10000000e-01, 6.20000000e-01, 6.30000000e-01,
# 6.40000000e-01, 6.50000000e-01, 6.60000000e-01,
# 6.70000000e-01, 6.80000000e-01, 6.90000000e-01,
# 7.00000000e-01, 7.10000000e-01, 7.20000000e-01,
# 7.30000000e-01, 7.40000000e-01, 7.50000000e-01,
# 7.60000000e-01, 7.70000000e-01, 7.80000000e-01,
# 7.90000000e-01, 8.00000000e-01, 8.10000000e-01,
# 8.20000000e-01, 8.30000000e-01, 8.40000000e-01,
# 8.50000000e-01, 8.60000000e-01, 8.70000000e-01,
# 8.80000000e-01, 8.90000000e-01, 9.00000000e-01,
# 9.10000000e-01, 9.20000000e-01, 9.30000000e-01,
# 9.40000000e-01, 9.50000000e-01, 9.60000000e-01,
# 9.70000000e-01, 9.80000000e-01, 9.90000000e-01,
# 1.00000000e+00, 1.01000000e+00])
#
#H = 1
#z = np.linspace(0, H,10)
#kv, kh, ks, kw = (10, 10, 10, 1)
#mv=1
#gamw = 10
#rw, rs, re = (0.03, 0.03, 0.5)
#drn = 1
#surcharge_vs_time = ((0,0.15, 0.3, 0.45,100.0), (0,50,50.0,100.0,100.0))
#tpor = t[np.array([20,60,90])]
#nterms = 20
#
#por, avp, settle = tangandonitsuka2000(z=z, t=t, kv=kv, kh=kh, ks=ks, kw=kw, mv=mv, gamw=gamw, rw=rw, rs=rs, re=re, H=H,
# drn=drn, surcharge_vs_time=surcharge_vs_time,
# tpor=tpor, nterms=nterms)
##################################################################
reader = ("""\
H = 1
drn = 1
dTv = 1 #dTv=kvref/mvref/gamw/H**2
#re=0.5, rw = 0.03, n = 16.6667, mu = 2.074475589,
#dTh = 2*khref/mvref/gamw/mu
dTh = 3.856396307
neig = 20
mvref = 1.0
kvref = 10.0
khref = 10.0
etref = 3.856396307 #2/mu/re**2
mv = PolyLine([0,1], [1,1])
kv = PolyLine([0,1], [1,1])
kh = PolyLine([0,1], [1,1])
et = PolyLine([0,1], [1,1])
dTw = 0.0003613006824568446 #dTv=kwref/mvref/gamw/H**2
kwref = 1
kw = PolyLine([0,1], [1,1])
surcharge_vs_depth = PolyLine([0,1], [1,1])
surcharge_vs_time = PolyLine([0,0.15,0.3,0.45,4],[0.0,50,50,100,100])
ppress_z = np.%s
avg_ppress_z_pairs = [[0,1]]
settlement_z_pairs = [[0,1]]
ppress_z_tval_indexes = [20,60,90]
tvals = np.%s
""" % (repr(z), repr(t)))
a = Speccon1dVRW(reader)
a.make_all()
#datafor no well resistance
avp_no_well = 100*np.array([[ 0.00324696, 0.00641694, 0.00953238, 0.0126017 , 0.01562987,
0.01862029, 0.02157548, 0.02449743, 0.02738778, 0.03024788,
0.05738761, 0.0822719 , 0.10525907, 0.12658293, 0.1464181 ,
0.16490438, 0.18215844, 0.19828034, 0.21335753, 0.22746753,
0.24067983, 0.25305715, 0.26465659, 0.27553032, 0.25547838,
0.23790104, 0.22198642, 0.2074141 , 0.19398549, 0.18155873,
0.17002455, 0.15929482, 0.14929611, 0.13996587, 0.13124986,
0.12310046, 0.11547534, 0.10833658, 0.10164995, 0.12563221,
0.14689894, 0.16627677, 0.18410003, 0.20058033, 0.21587175,
0.23009504, 0.2433491 , 0.25571746, 0.26727216, 0.27807632,
0.28818593, 0.29765116, 0.30651729, 0.31482546, 0.29236538,
0.27252759, 0.25449115, 0.2379271 , 0.22262886, 0.20844708,
0.19526545, 0.18298923, 0.1715388 , 0.1608458 , 0.15085055,
0.14150028, 0.13274787, 0.1245509 , 0.11687089, 0.10967276,
0.10292438, 0.09659617, 0.09066084, 0.08509314, 0.07986962,
0.0749685 , 0.07036946, 0.06605359, 0.06200322, 0.05820182,
0.05463397, 0.05128519, 0.04814195, 0.04519158, 0.04242218,
0.03982263, 0.03738247, 0.03509191, 0.03294176, 0.0309234 ,
0.02902874, 0.02725019, 0.02558063, 0.02401338, 0.02254216,
0.02116109, 0.01986464, 0.01864762, 0.01750516, 0.01643271,
0.01542596, 0.01448089, 0.01359372, 0.0127609 , 0.01197911,
0.01124522, 0.01055628, 0.00990956, 0.00930246, 0.00873255]])
por_no_well = np.array(
[[ 0. , 0. , 0. ],
[ 10.62834433, 5.71540426, 0.79195768],
[ 18.10955225, 11.14818494, 1.55981113],
[ 23.22767635, 16.0566849 , 2.2801995 ],
[ 26.62643019, 20.26892536, 2.93122316],
[ 28.80909111, 23.69187844, 3.49311208],
[ 30.15548187, 26.3014876 , 3.94882356],
[ 30.93852215, 28.11965758, 4.28455203],
[ 31.33977648, 29.18687894, 4.49013755],
[ 31.4624026 , 29.5381209 , 4.55936353]])
settle_no_well = (np.interp(t,[0,0.15,0.3,0.45,4], [0.0,50,50,100,100]) - avp_no_well)
# custom plots
title = ("Tang and Onitsuka (2000) vertical and radial drainage including well resistance")
fig = plt.figure(figsize=(13,6))
fig.suptitle(title)
#z vs u
ax1 = fig.add_subplot("131")
ax1.set_xlabel('Excess pore pressure, kPa')
ax1.set_ylabel('Depth')
ax1.invert_yaxis()
ax1.plot(por, z,
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax1.plot(a.por, z,
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
ax1.plot(por_no_well, z,
ls="None", color='green', marker="+", ms=5,
label='no well resis')
# avp vs t
ax2 = fig.add_subplot("132")
ax2.set_xlabel('Time')
ax2.set_ylabel('Average excess pore pressure, kPa')
ax2.set_xscale('log')
ax2.set_xlim((0.01, 10))
ax2.plot(t, avp[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax2.plot(t, a.avp[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
ax2.plot(t, avp_no_well[0],
ls="None", color='green', marker="+", ms=5,
label='no well resis')
# settlement vs t
ax3 = fig.add_subplot("133")
ax3.set_xlabel('Time')
ax3.set_ylabel('Settlement')
ax3.invert_yaxis()
ax3.set_xscale('log')
ax3.set_xlim((0.01, 10))
ax3.plot(t, settle[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax3.plot(t, a.set[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
ax3.plot(t, settle_no_well[0],
ls="None", color='green', marker="+", ms=5,
label='$k_w=\\infty$')
leg = ax3.legend()
leg.draggable()
fig.subplots_adjust(top=0.90, bottom=0.15, left=0.1, right=0.94, wspace=0.4)
#fig.tight_layout()
plt.show()
(Source code, png, hires.png, pdf)