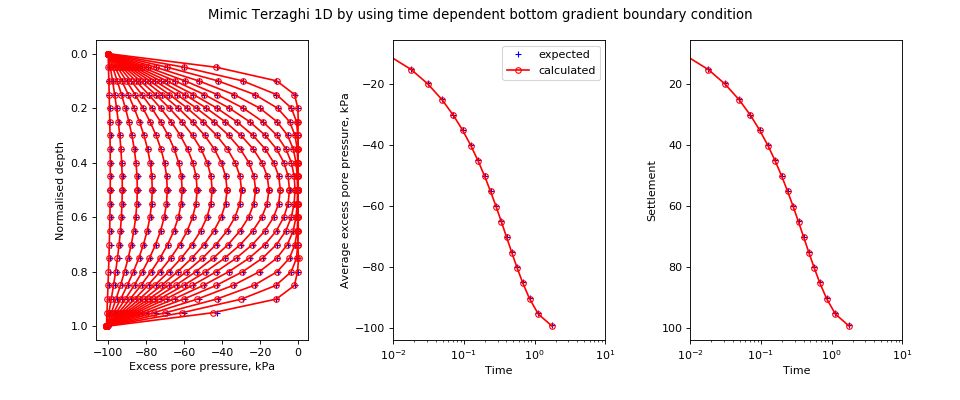
speccon example code: speccon1d_vr_mimic_terzaghi_with_gradient_bottom_boundary_condition.py¶
# speccon1d_vr example (if viewing this in docs, plots are at bottom of page)
# Mimic Terzaghi pervious top pervious bottom 1D vertical consolidation
# by specifying a time dependent gradient boundary condition at the base.
# The pore pressure at the top instantly reduces to -100 kPa. The gradient at
# the base is prescribed according to theflow rate calculated from
# conventional Terzaghi 1D consolidation. The resulting pore pressure
# profile should be [Terzahgi PTPB] - [100 kPa].
# This file should be run with python. It will not work if run with the
# speccon1d_vr.exe script program.
from __future__ import division, print_function
import numpy as np
from geotecha.speccon.speccon1d_vr import Speccon1dVR
import matplotlib.pyplot as plt
# TERZ1D_T = time values
# TERZ1D_AVP = Terzaghi 1d average excess pore pressures corresponding to
# times in TERZ1D_T. Properties are: cv=1, H=1, u0=1
# TERZ1D_Z = z/H values
# TERZ1D_POR = excess p.pressure values at depths TERZ1D_Z and times TERZ1D_T
TERZ1D_T = np.array([0.008, 0.018, 0.031, 0.049, 0.071, 0.096, 0.126,
0.159, 0.197, 0.239, 0.286, 0.34, 0.403, 0.477, 0.567,
0.684, 0.848, 1.129, 1.781])
TERZ1D_AVP = np.array(
[[ 0.8990747 , 0.84861205, 0.80132835, 0.75022262, 0.69933407,
0.65038539, 0.59948052, 0.55017049, 0.49966188, 0.44989787,
0.40039553, 0.35035814, 0.2998893 , 0.24983377, 0.20008097,
0.14990996, 0.10002108, 0.05000091, 0.01000711]])
TERZ1D_Z = np.array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,
0.7, 0.8, 0.9, 1. ])
TERZ1D_POR = np.array(
[[ 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ],
[ 0.5708047 , 0.40183855, 0.31202868, 0.25060581, 0.209277 ,
0.18051017, 0.15777238, 0.1401947 , 0.12492869, 0.11139703,
0.09868545, 0.08618205, 0.07371295, 0.0613951 , 0.04916581,
0.03683692, 0.02457785, 0.01228656, 0.00245901],
[ 0.8861537 , 0.70815945, 0.57815202, 0.47709676, 0.40440265,
0.35188372, 0.30934721, 0.27584089, 0.24631156, 0.21986645,
0.19487593, 0.17022241, 0.145606 , 0.12127752, 0.09712088,
0.07276678, 0.04855051, 0.02427058, 0.00485748],
[ 0.98229393, 0.8861537 , 0.77173068, 0.66209592, 0.57402972,
0.50633278, 0.44919934, 0.40274312, 0.36079264, 0.322593 ,
0.28615206, 0.25003642, 0.21390512, 0.17817202, 0.14268427,
0.10690487, 0.07132769, 0.03565698, 0.00713634],
[ 0.9984346 , 0.96498502, 0.89182244, 0.79866319, 0.71151086,
0.63842889, 0.57300943, 0.5173496 , 0.46536864, 0.41697458,
0.37024076, 0.32365106, 0.27692667, 0.23067729, 0.18473404,
0.13841059, 0.09234855, 0.04616539, 0.00923947],
[ 0.99992277, 0.99159201, 0.95536184, 0.8897753 , 0.81537699,
0.74554825, 0.67795464, 0.61693194, 0.55750293, 0.50070214,
0.44507671, 0.38925529, 0.33311924, 0.27750057, 0.22223477,
0.16650815, 0.11109548, 0.05553705, 0.0111151 ],
[ 0.9999979 , 0.9984346 , 0.9840325 , 0.94470726, 0.88846498,
0.82769841, 0.76271322, 0.69962982, 0.63517948, 0.57181325,
0.50885214, 0.44524423, 0.38110176, 0.3174894 , 0.25426314,
0.19050572, 0.12710688, 0.0635412 , 0.01271704],
[ 0.99999997, 0.99977515, 0.99506515, 0.97461982, 0.93621426,
0.88684221, 0.82720628, 0.76436582, 0.69689722, 0.62871883,
0.5600537 , 0.49025645, 0.41969701, 0.34965996, 0.28003063,
0.2098124 , 0.13998847, 0.06998076, 0.01400585],
[ 1. , 0.99997517, 0.99868444, 0.9892702 , 0.96479424,
0.92594095, 0.87215551, 0.81066205, 0.74161724, 0.67020692,
0.59748729, 0.52320368, 0.44795959, 0.37322105, 0.29890288,
0.2239528 , 0.14942309, 0.07469716, 0.01494978],
[ 1. , 0.99999789, 0.99968908, 0.99551731, 0.97956541,
0.94796078, 0.89856843, 0.83840947, 0.76868357, 0.69543129,
0.62029292, 0.54329327, 0.46519818, 0.3875934 , 0.31041531,
0.23257876, 0.15517842, 0.07757427, 0.0155256 ],
[ 1. , 0.99999973, 0.99988166, 0.9971974 , 0.98407824,
0.95504225, 0.90726835, 0.8476479 , 0.77774256, 0.70389411,
0.62795246, 0.55004364, 0.47099154, 0.39242376, 0.31428453,
0.23547787, 0.15711273, 0.07854125, 0.01571913]])
# flow_t = times values for time-dependent bottom gradient boundary
# flow_v = velocity values for time-dependent bottom gradient boundary
flow_t = np.array([ 0, 0.00000000e+00, 1.00000000e-05, 1.32571137e-05,
1.75751062e-05, 2.32995181e-05, 3.08884360e-05,
4.09491506e-05, 5.42867544e-05, 7.19685673e-05,
9.54095476e-05, 1.26485522e-04, 1.67683294e-04,
2.22299648e-04, 2.94705170e-04, 3.90693994e-04,
5.17947468e-04, 6.86648845e-04, 9.10298178e-04,
1.20679264e-03, 1.59985872e-03, 2.12095089e-03,
2.81176870e-03, 3.72759372e-03, 4.94171336e-03,
6.55128557e-03, 8.68511374e-03, 1.15139540e-02,
1.52641797e-02, 2.02358965e-02, 2.68269580e-02,
3.55648031e-02, 4.71486636e-02, 6.25055193e-02,
8.28642773e-02, 1.09854114e-01, 1.45634848e-01,
1.93069773e-01, 2.55954792e-01, 3.39322177e-01,
4.49843267e-01, 5.96362332e-01, 7.90604321e-01,
1.04811313e+00, 1.38949549e+00, 1.84206997e+00,
2.44205309e+00, 3.23745754e+00, 4.29193426e+00,
5.68986603e+00, 7.54312006e+00, 1.00000000e+01])
# flow_v comes from geotecha.consolidation.terzahgi module:
# terzaghi_1d_flowrate(z=np.array([0.0]), t=flow_t, kv=10, mv=1, gamw=10, ui=100, nterms=500)
flow_v = -np.array([ 0.00000000e+00, 1.00000000e+05, 1.78412412e+04,
1.54953209e+04, 1.34578624e+04, 1.16883065e+04,
1.01514272e+04, 8.81663000e+03, 7.65734340e+03,
6.65048985e+03, 5.77602610e+03, 5.01654435e+03,
4.35692582e+03, 3.78403963e+03, 3.28648146e+03,
2.85434652e+03, 2.47903242e+03, 2.15306785e+03,
1.86996392e+03, 1.62408493e+03, 1.41053624e+03,
1.22506677e+03, 1.06398442e+03, 9.24082570e+02,
8.02576220e+02, 6.97046575e+02, 6.05392880e+02,
5.25790600e+02, 4.56655118e+02, 3.96610163e+02,
3.44460438e+02, 2.99167808e+02, 2.59830644e+02,
2.25665819e+02, 1.95991124e+02, 1.70184572e+02,
1.47532018e+02, 1.26954815e+02, 1.07034205e+02,
8.66871910e+01, 6.59246745e+01, 4.59181293e+01,
2.84338280e+01, 1.50624045e+01, 6.48748315e+00,
2.12376806e+00, 4.83256782e-01, 6.78952680e-02,
5.03366995e-03, 1.59915607e-04, 1.65189842e-06,
3.84807183e-09])
# adjust depth values for PTPB
z = np.append(0.5*TERZ1D_Z, 1 - 0.5*TERZ1D_Z[::-1])
t = TERZ1D_T
# expected results
por = 100 * np.vstack((TERZ1D_POR, TERZ1D_POR[::-1,:])) - 100
avp = 100 * TERZ1D_AVP - 100
settle = 100 * (1 - TERZ1D_AVP)
# the reader string is a template with {} indicating where parameters will be
# inserted. Use double curly braces {{}} if you need curly braces in your
# string.
reader = ("""\
H = 1
drn = 1
dTv = 1 * 0.25
neig = 15
mvref = 1.0
mv = PolyLine([0,1], [1,1])
kv = PolyLine([0,1], [1,1])
#note: combo of dTv, mv, kv essentially gives dTv = 1
top_vs_time = PolyLine([0, 0.0, 5], [0,-100,-100])
bot_vs_time = PolyLine([0, 0.0, 5], [0,-100,-100])
bot_vs_time = PolyLine(np.%s, np.%s)
ppress_z = np.%s
avg_ppress_z_pairs = [[0,1]]
settlement_z_pairs = [[0,1]]
tvals = np.%s
""" % (repr(flow_t), repr(flow_v*2), repr(z),repr(t)))
# we use flow_v*2 because flow_v on it's own is for flowrate of
# terzaghi PTIB where h=H = 1. for this test we have basically have 2 layers
# each of h=0.5. Thus we divide dTv by 4. The flow_v data is du/dz.
# because H was unity du/dz = du/Dz. when h=0.5 we need to multiply flow_v
# 2 to get the same gradient at the base
a = Speccon1dVR(reader)
a.make_all()
# custom plots
title = ("Mimic Terzaghi 1D by using time dependent bottom "
"gradient boundary condition")
fig = plt.figure(figsize=(12,5))
fig.suptitle(title)
#z vs u
ax1 = fig.add_subplot("131")
ax1.set_xlabel('Excess pore pressure, kPa')
ax1.set_ylabel('Normalised depth')
ax1.invert_yaxis()
ax1.plot(por, z,
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax1.plot(a.por, z,
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
# avp vs t
ax2 = fig.add_subplot("132")
ax2.set_xlabel('Time')
ax2.set_ylabel('Average excess pore pressure, kPa')
ax2.set_xscale('log')
ax2.set_xlim((0.01, 10))
ax2.plot(t, avp[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax2.plot(t, a.avp[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
leg = ax2.legend()
leg.draggable()
# settlement vs t
ax3 = fig.add_subplot("133")
ax3.set_xlabel('Time')
ax3.set_ylabel('Settlement')
ax3.invert_yaxis()
ax3.set_xscale('log')
ax3.set_xlim((0.01, 10))
ax3.plot(t, settle[0],
ls="None", color='Blue', marker="+", ms=5,
label='expected')
ax3.plot(t, a.set[0],
ls='-', color='red', marker='o', ms=5, markerfacecolor='None',
markeredgecolor='red',
label='calculated')
fig.subplots_adjust(top=0.90, bottom=0.15, left=0.1, right=0.94, wspace=0.4)
#fig.tight_layout()
plt.show()
(Source code, png, hires.png, pdf)